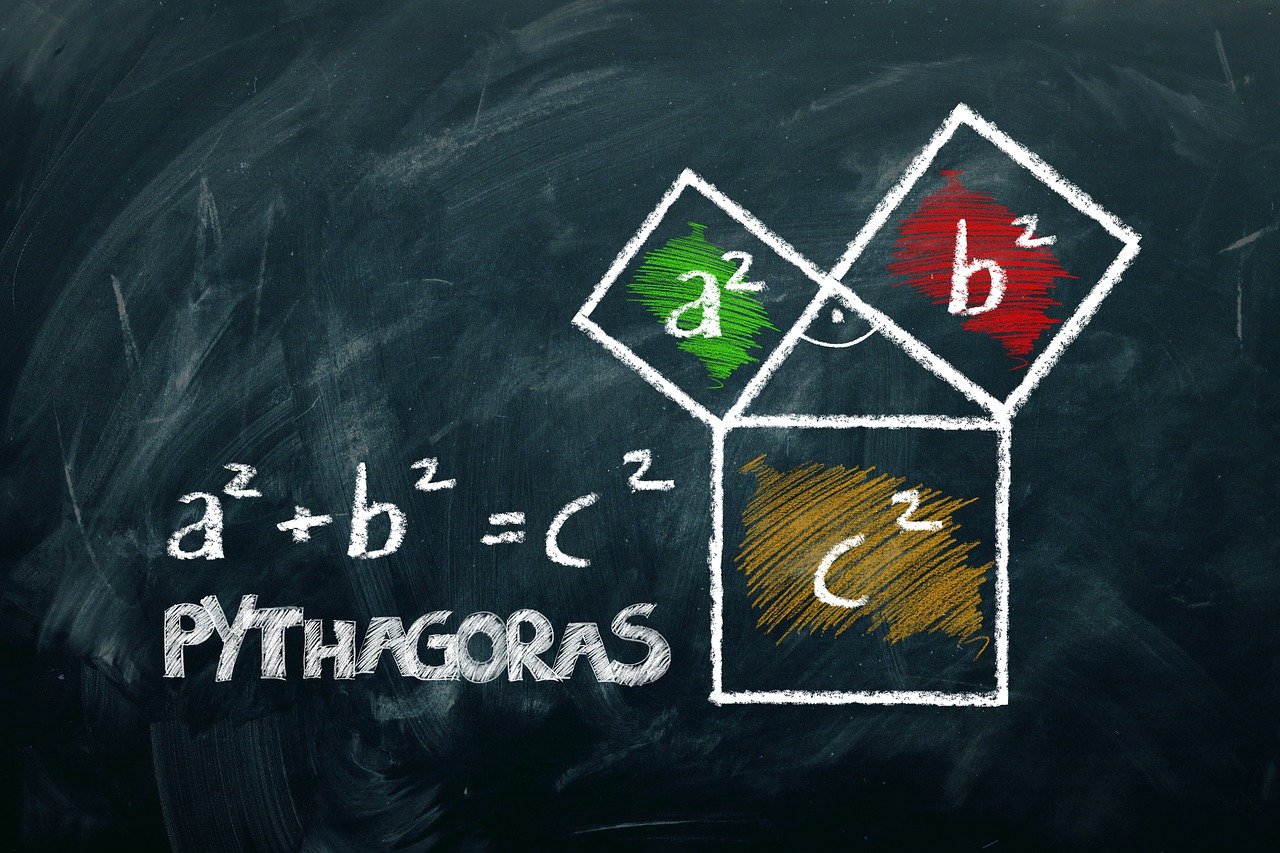The Pythagoras theorem is named after a renowned Greek mathematician called Pythagoras. Pythagoras Theorem is a significant and widely used topic in mathematics, which states down the connection between the sides that helps us find the area of right triangle. It is also identified as the Pythagorean Theorem. The formula and the evidence of Pythagoras theorem are explained below with examples:
Pythagoras theorem is mainly done to find the length of a particular side and angle of the triangle. By applying this theorem, we can determine the base, perpendicular, and hypotenuse formulas. Now let us examine the concepts of the Pythagorean theorem in brief.
Pythagoras Theorem
Pythagoras theorem proves that in any provided right-angled triangle, the square of the hypotenuse side is identical and exactly equal to the sum of squares of the other two sides of the given triangle. The sides of the triangle are distinguished as perpendicular, the base, and the hypotenuse. Here, the hypotenuse is the tallest side and is opposite to the 90-degree angle. The sides of a right triangle which have only positive integer units, when squared, are put in an equation, thus termed as a Pythagorean triple.
Pythagoras Theorem Formula
The standard given formula for the Pythagoras theorem is given here below:
In a triangle let us take P which is the perpendicular side, where B is the base of the triangle, H is the hypotenuse side. Thus, according to the meaning, the Pythagoras Theorem formula is given as:
Hypotenuse^2 = Perpendicular^2 + Base^2
Where can we use Pythagoras Theorem?
- To identify if the given triangle is a right-angled triangle or not
- In a right-angled triangle, we can determine the length of any side if the other two sides of the triangle are given
- To obtain the diagonal or the slope of a square
- In oceanography, the formula of the theorem is used to assume the speed of sound waves in the water
- Pythagoras theorem is used in climatology and aerospace to determine the sound source and its range in space
- We can use the Pythagoras theorem to find automatic components such as tv screens, computer screens, solar panels, etc
- We can use the Pythagorean Theorem to find the angle of a particular landscape
- In navigation, the theorem is used to find the most concise distance between two given points
- In building and construction, we can use the Pythagorean theorem to find the slope of a roof, drainage system, light posts, etc
What is the use of Pythagoras theorem?
The Pythagoras theorem can be used to find the steepness of the incline of the hills or mountain ranges. It can also be practiced to find the distance between an observer on a given height and a point on the ground from the tower or a building beyond which the observer is viewing the point. It is mostly used in the domains of construction and architecture.
Proving the theorem by oneself
- Get a paper pen and scissors, then with the help with these following steps:
- Trace a right-angled triangle on paper and leave plenty of space
- Trace a square along the hypotenuse which is the longest side of a triangle
- Paint the same sized square on the other side of the hypotenuse drawn
- Trace lines along the square
- Then carve out the shapes
- Systematize the shapes so that you can prove that the big square has the same area as the two squares on the other sides. Thus, demonstrating Pythagoras theorem
Conclusion
Pythagoras is attributed to several educational topics in mathematics, astronomy, music, religion, philosophy, etc. One of his celebrated contributions to mathematics is the development and the provision of the Pythagorean Theorem. Cuemath is an online learning platform that helps students magnify their geometrical and graphical skills while exploring Pythagoras theorem. Cuemath uses modern teaching methods in order to make learning more engaging. The Pythagorean theorem also prepares students for advanced math and will help establish and solidify their concepts in mathematics.